Model
Overview
Progenie is introduced to a prokaryotic population via phage then spreads throughout that population via bacterial conjugation, eliminating the target gene from the genome of each cell as it spreads. The success of Progenie is wholly dependent on the extent of that secondary spread. Because of this, we developed a statistical model of the spread of φMINTO through a population of mcherry-expressing E. coli. We started with an SEIR model, then modified it to reflect the representative parts and dynamics of our target population.
Our modeling goals:
As this first model was run before we could test our infection and conjugation mechanisms experimentally, the values for each parameter used in this run were gathered from relevant literature. As we collect data in future wet lab experiments, we will iteratively adjust those parameter values and improve our model.
Insights we gain from this model will be used to further inform our experimental design as we shift from the mCherry towards using Progenie in real-world applications.
Our model is based on an SEIR model
This model is an adaptation of an
In the standard SEIR model, there are 4 compartments, each representing the proportion of the population that fits the following categories:
The SEIR compartment model is built to determine differential equations for the rate of change of each compartment. Those equations are then used to run simulations of the pathogen’s spread throughout a population; the simulation can be used to determine if a pathogen will invade a population or die out, and how quickly, under a variety of circumstances.
Progenie mCherry Compartment Model
Although Progenie is not an infectious disease, the ability of F+, F’, and HFR cells to conjugate φMINTO to F- cells makes our plasmid spread similar to an infectious agent. For more information on conjugation and F-status, see our
In our experimental chromosomally-integrated mCherry model, we modified the standard SEIR model described above into a three-compartment model. The new compartments are:
And the rates that change the composition of those compartments are:
In this model, we expect that cells from I conjugate φMINTO into cells from S, causing those individuals to leave the S group and join the E group. For Progenie to be completely successful, the S group must be eliminated, leaving a population made up of only E and I.

Figure 1: Compartment model depicting the transmission dynamics of the φMINTO plasmid in a bacterial population. Each compartment represents the population count of a celltype. The red compartment S represents the count of cells that are susceptible to conjugation (F-), contain the target gene, and do not yet carry φMINTO. In our mCherry model, these are the DH5α--mcherry cells. The top purple box I represents the count of cells initially transfected with φMINTO and that can spread the plasmid to S cells via conjugation (F+, F’, or HFR). The purple box E represents the count of transconjugant cells, having received φMINTO through bacterial conjugation but unable to conjugate the plasmid to others. Thick arrows are the rate of movement of individuals from one compartment into another. Thin arrows show the role one compartment plays in the changing of another compartment.
Assumptions
The most important rate of the model is the rate of conjugation. This rate is highly variable, depending on the relatedness of the species interacting, cell density, mating time, plasmid size, and many environmental conditions [1]. In a study by Alderliesten et. al, the highest and lowest frequencies of conjugation differed by 11 orders of magnitude. With such fluctuation, we could not expect a computational model to be relevant for all instances of Progenie. In our experimental “mixed” culture, all cells are only DH5a and DH5a F’ E. coli; in future applications in the environment, a population will include a wide variety of species. Thus, this computational model is tailored to our mCherry experiments involving conjugation between strains of E. coli, rather than future applications to different pathogens across mixed-cultures of varying strain and species composition.
For our model, we make the following assumptions:
Variables:
| |
Number of cells for a carrying capacity |
|---|---|
| |
Number of cells in the Susceptible population |
| |
Number of cells in the Infected population |
| |
Number of cells in the Exposed population |
| |
Sum of all cells ( |
Depending on if we model using a carrying capacity or perpetual exponential growth, N may be the sum of all cells in the population, else
Parameters:
| |
"Birth" rate |
|---|---|
| |
Conjugation rate |
| |
Death rate of susceptible cells (natural) |
| |
Death rate of infected cells (possibly accelerated) |
Using a series of formulas we derive rates for our model and plug in literature-derived constants. Converting from the exponential function to an ordinary differential equation, we can derive a formula to determine the percent change per generation from a doubling time in generations:

From a generational percent change, we can determine a rate as follows:

Following our assumption that E. coli doubling time is 20 min when not limited by nutrients or space, we set our generational change as 20 min, as such the percent increase in cells per generation is 1.0 (100%) and the birth rate (B) is 0.693. Following a similar procedure, we convert the constant death rate (mu) of 2.7% per generation in the absence of the SOS response to a rate of 0.0266. Alpha may vary from mu as the death rate of cells with the Progenie system may die at a faster rate or grow slower [2].
Equations:

Results
Following the aforementioned assumptions and in the context of our experiments, we simulate 8 hours (24 generations) runs of Progenie. Interactions between cells follow as depicted in the figure with birth and death rates described above. Note that our wet lab experiments are not a mixed-culture as we are only working with two strains of NEB DH5DH5α cells: F- and F’. Model parameters we may alter include initial population sizes of I and S, the death rate of cells containing φMINTO (alpha), carrying capacity (K), and conjugation rate (C).
Our code is available

Figure 2: Graph of raw cell counts with SIE lines
Conclusions
Using a birth, death, and conjugation rate derived from literature, our model demonstrated the success of Progenie to fully propagate into a susceptible population [Fig 3 & 4 ].
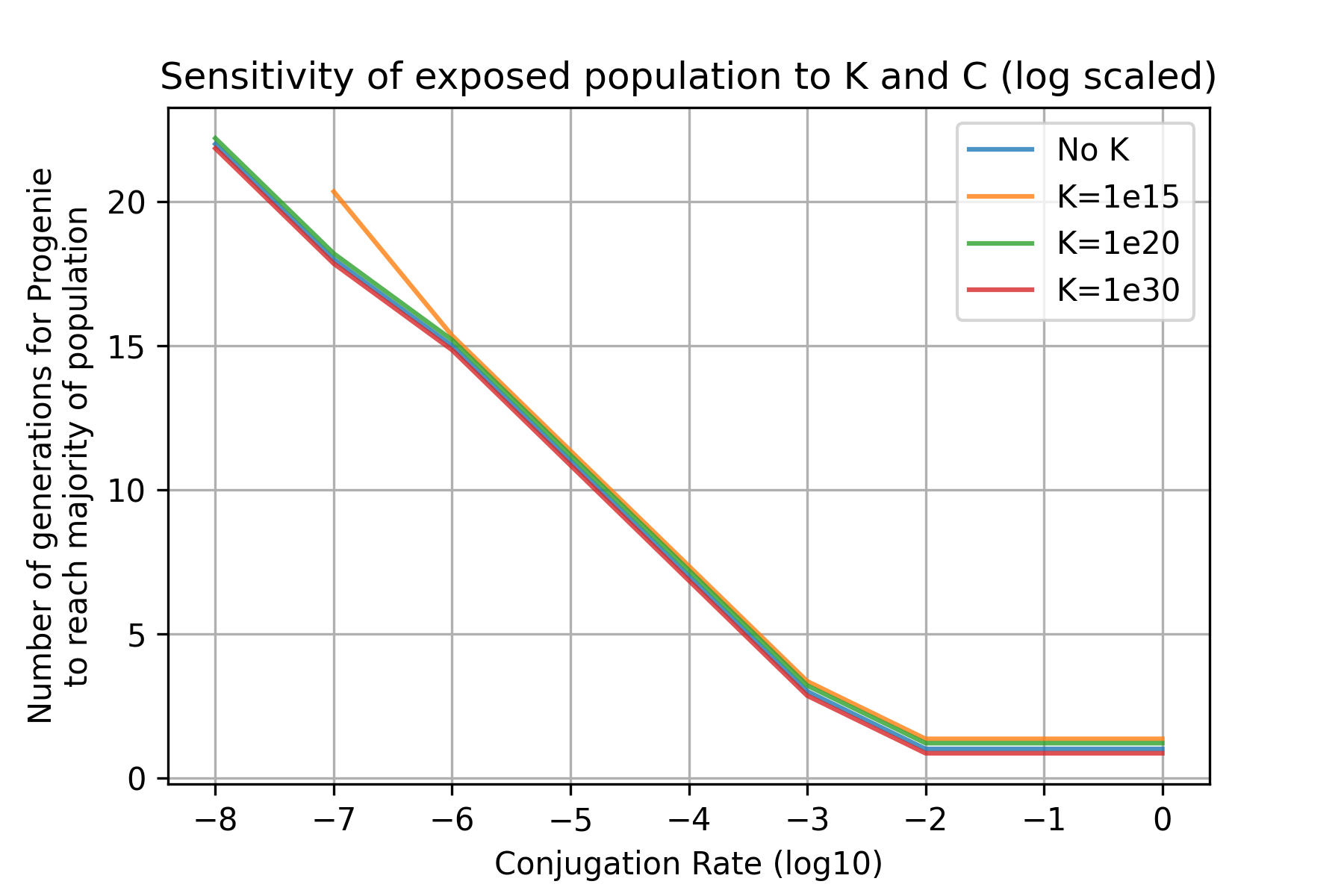
We then varied conjugation rates to determine the lower bounds of conjugation efficiency that must be required for Progenie success. We measure success as the Exposed population reaching a relative majority in the timeframe of 8 hours. Modeling 16 conjugation rates across 4 values for carrying capacity, we found that a conjugation rate of 1e-10 is required for our system to succeed for reasonable carrying capacities [Fig 5].
At lower carrying capacities and conjugation rates, Progenie does not have sufficient time to spread fully in a population. We modeled this using a conjugation rate of 1e-10, where 8 hours was not sufficient for E to reach a relative maximum; when the model timeframe was increased to 10 hours, we found success [Fig 6].
Using our base model, we then varied parameters to explore necessary values for minimum cell death and initial infectious population. We increased the death rate of cells containing φMINTO by over a magnitude of the literature derived death of 2.7% and found that in this model as long as cell death for the infectious population is under 28% per generation, Progenie would succeed within the 8 hour time frame. By varying the initial infectious cell population, we found that the ratio of donor : recipient cells is 3:1e10. This means that even a smaller phage dose will ensure Progenie success in the system.
Progenie proliferated in our simulated mixed population.
Our models demonstrate that Progenie will be successful in an experimental setting as the parameters at which Progenie fails is beyond what can be expected in normal use cases. Across the range of parameters we tested, Progenie either fully propagates to 99.99+% of the population or is unable to reach an inflection point and is lost in the system. The 8 hour cutoff means that we don’t always fully simulate and visualize the system to steady-state, but additional tests to 100 generations demonstrate that Progenie either fully proliferates or is lost.
The simulation depicted in [Fig 7] involves lower than expected conjugation rates and higher than expected death rate to demonstrate a possible scenario of Progenie failing to fully propagate with the φMINTO exposed population outcompeted by the still susceptible population. Our simulations with biologically relevant parameters maintain that Progenie will be successfully proliferated.
How long it takes Progenie to succeed is heavily dependent on the conjugation rate.
From our simulations depicted in [Fig 5] and our conclusions from the range of conjugation efficiencies, we determine that Progenie is effective in the space of 22 generations, or roughly 7.5 hours. Progenie may reach a majority in fewer generations, but generally within the first 8 hour period is when Progenie acts within a system. Beyond this time point, growth and spread of Progenie is constrained by carrying capacity.
Summary and Future Directions:
Our mathematical model simulating Progenie with biologically-relevant, literature-derived parameters supports that Progenie will be successful in propagating in a mixed population of cells within a reasonable timeframe.
We first simulated Progenie with relevant parameters and discovered that the demonstrates success in Progenie proliferation. We then tested a range of parameters including initial population of conjugative donors, death rate, carrying capacity, and conjugation rate and found that
In the future, we plan to expand our model to incorporate more compartments involving varying cell types and F-status. This will allow us to more accurately model applications within a more complicated environment. We may explore additional scenarios in which recipients may become conjugative donors or that the initial infectious population may lose φMINTO. Nonetheless, from the robustness and effectiveness of Progenie in our current simulations, we expect Progenie will be applicable and successful in varied situations.